Finding missing angles in congruent triangles worksheet

In this explainer, we will learn how to use the triangle congruence criteria SSS, SAS, ASA, and RHS to find unknown angles or sides in geometry problems.

We can recall that there are many different ways of determining whether two triangles are congruent. For example, we can check whether they have three congruent sides, have two congruent sides and the included angles are congruent, or have two congruent angles and the shared sides are congruent. These are called the SSS, SAS, and ASA congruence criteria respectively.

Finally, there is an extra congruence criterion for right triangles called the RHS criterion, which says that any two right triangles with congruent hypotenuses and any congruent side must be congruent.

We can use these congruence criteria to determine if two triangles are congruent, which shows that their corresponding sides and angles are congruent. This means we can find unknown angles and sides by using triangle congruency.

Let’s see an example of using congruent triangles to prove a geometric property by considering the diagonals of a parallelogram. We recall that a parallelogram 𝐴𝐵𝐶𝐷 is a quadrilateral with opposite sides that are parallel and have the same length. We can note that one diagonal of this parallelogram splits the shape into two triangles: △𝐴𝐶𝐷 and △𝐶𝐴𝐵.

We can see that both triangles have three congruent sides: 𝐶𝐷=𝐴𝐵,𝐴𝐷= 𝐶𝐵,𝐴𝐶=𝐶𝐴().c ommonside

Hence, the triangles are congruent by the SSS criterion. Therefore, the corresponding angles in the triangles are congruent, so 𝑚∠𝐵𝐴𝐶=𝑚∠𝐷𝐶𝐴 and 𝑚∠𝐵𝐶𝐴=𝑚∠𝐷𝐴𝐶.

We can do the same with the other diagonal as shown.

If we sketch both diagonals on the parallelogram and label the point of intersection between the diagonals 𝐸, then we can note that triangles △𝐴𝐷𝐸 and △𝐶𝐵𝐸 have two congruent angles and the included side is congruent.

Thus, they are congruent by the ASA criterion. This means that their corresponding sides are congruent, so 𝐷𝐸=𝐵𝐸 and 𝐴𝐸=𝐸𝐶.

Hence, we have shown that the diagonals of a parallelogram bisect each other.

Let’s now see another example of showing a useful geometric property by using triangle congruence.

Example 1: Applying Properties of Congruence to Solve Problems

In the figure, △𝐴𝐵𝐶 and △𝐸𝐹𝐷 are congruent.

1. Work out the length of 𝐵𝐶.
2. Work out the length of 𝐸𝐹.
3. Work out measure of angle 𝐷𝐸𝐹.

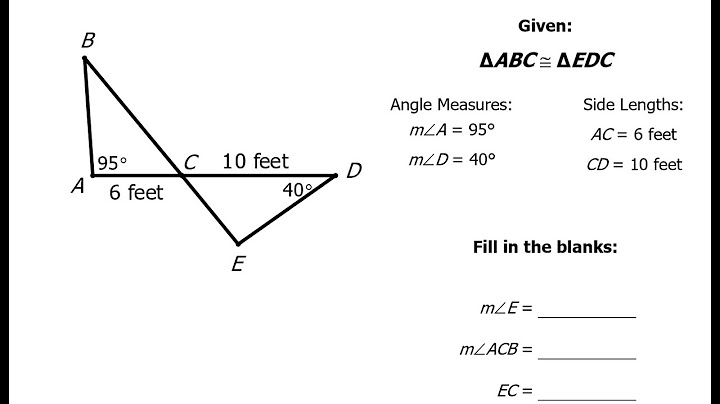
Answer

We start by recalling that we say that two polygons are congruent if their corresponding side lengths and angles are congruent. Since we are told that triangles △𝐴𝐵𝐶 and △𝐸𝐹𝐷 are congruent, we can conclude that their corresponding sides have the same length and their corresponding angles have the same measure.

In congruence, the order we write the vertices in tells us the corresponding sides and angles. We can also see this in the diagram.

We have 𝐴𝐵=𝐸𝐹,𝐵𝐶=𝐹𝐷,𝐶𝐴=𝐷𝐸.

Part 1

Using the congruence of the two triangles, we know that 𝐵 𝐶 is the same length as 𝐹𝐷. Since 𝐹𝐷=4.5, we must have 𝐵𝐶=4.5.

Part 2

Using the congruence of the two triangles, we know that 𝐸𝐹 is the same length as 𝐴𝐵. Since 𝐴𝐵=2.2, we must have 𝐸𝐹=2.2.

Part 3

Using the congruence of the two triangles, we know that the interior angle at 𝐴 must have equal measure to the interior angle at 𝐸 since these are corresponding angles.

Since 𝑚∠𝐶𝐴𝐵= 63.4,∘ we must also have 𝑚 ∠𝐷𝐸𝐹=63.4.∘

In our next example, we will use the congruency of triangles to find the measure of an angle in a given diagram.

Example 2: Finding the Measure of an Angle in a Triangle Using RHS Congruence

In the following figure, find 𝑚∠𝐽 𝐾𝐿.

Answer

We note that the diagram contains two right triangles: △𝐽𝐾𝐿 and △𝑀𝐾𝐿. We can also see that 𝐽𝐿=𝑀𝐿 and these triangles share side 𝐾𝐿.

We recall that the RHS criterion for triangle congruency tells us that if right triangles have congruent hypotenuses and one side congruent, then they are congruent. Hence, △𝐽 𝐾𝐿≅△𝑀𝐾𝐿 by the RHS criterion.

This means that their corresponding angles and side lengths are congruent. We note that ∠𝐽𝐾𝐿 corresponds to ∠𝑀𝐾𝐿, so both angles have the same measure.

Hence, 𝑚∠𝐽𝐾𝐿=34.∘

In our next example, we will find the lengths of multiple sides in a geometric construction by using triangle congruence.

Example 3: Finding a Side Length in a Triangle Using ASA Congruence

Find the length of 𝐴𝐷 and 𝐷𝐶.

Answer

We first note that we are given the measures of two interior angles of each triangle and that these measures are equal: 𝑚∠𝐴𝐶𝐵=𝑚∠𝐷𝐸𝐶=31,𝑚∠𝐶𝐵𝐴=𝑚∠𝐸𝐶𝐷=68.∘∘

Similarly, we can notice that the included sides of these angles are equal in length since 𝐵𝐶=𝐸𝐶=5.7.cm

So, the two triangles have two angles of equal measure, and the included sides are congruent. Hence, by the ASA congruence criterion, we have △𝐴𝐵𝐶≅△𝐷𝐶𝐸.

This means that their corresponding sides and angles must be congruent. We see that side 𝐷𝐶 corresponds to 𝐴𝐵. So, these sides are the same length.

Thus, 𝐷𝐶=3cm.

We also note that 𝐴𝐶 corresponds to 𝐷𝐸, so these line segments have the same length. Adding this length and the length of 𝐷𝐶 onto the diagram gives us the following.

We see that 𝐴𝐷=𝐴𝐶−𝐷𝐶. Hence, 𝐴𝐷=5.4−3=2.4.cm

Therefore, 𝐴𝐷=2.4cm and 𝐷𝐶=3cm.

In our next example, we will determine the measure of an angle by using the congruency of triangles.

Example 4: Finding the Measure of an Internal Angle Using SAS Congruence and Complementary Angles

Given that 𝐴𝐵𝐶𝐷 is a square, find 𝑚∠𝑌𝐶𝐵.

Answer

We first note that we are given two congruent line segments: 𝐶𝑋 and 𝐵𝑌. We can use this and the fact that 𝐴𝐵𝐶𝐷 is a square to show that triangles 𝑌𝐵𝐶 and 𝑋𝐶𝐷 are congruent.

Since 𝐴𝐵𝐶𝐷 is a square, we can add right angles at the vertices of the square. Similarly, the sides of a square are all the same length, so 𝐵𝐶=𝐶𝐷. This gives us the following.

We see that triangles 𝑌𝐵𝐶 and 𝑋𝐶𝐷 are both right triangles with congruent legs. In particular, we have 𝑌𝐵=𝑋𝐶,𝐵𝐶=𝐶𝐷,𝑚∠𝑌𝐵𝐶=𝑚∠𝑋𝐶𝐷=90.∘

This means that they have congruent sides and congruent included angles, so they are congruent by the SAS criterion.

We note that ∠𝐷=90∘ since it is the interior angle of a square. We can determine 𝑚∠𝑋𝐷𝐶 by noting it adds to 56∘ to give a right angle. So, 90=56+𝑚∠𝑋𝐷𝐶𝑚∠𝑋𝐷𝐶=90−56=34.∘∘∘∘∘

We can add this onto the diagram.

Since △𝑌𝐵𝐶≅△𝑋𝐶𝐷, their corresponding angles are congruent. We note that ∠𝑋𝐷𝐶 corresponds to ∠𝑌𝐶𝐵, so their measures are equal.

Hence, 𝑚∠𝑌𝐶𝐵=34. ∘

In our final example, we will find missing lengths in a kite by using triangle congruence.

Example 5: Finding Missing Lengths by Applying ASA Congruence

Find the lengths of 𝐶𝐵 and 𝐴𝐷.

Answer

We begin by noting that we are given pairs of congruent angles in the diagram: 𝑚∠𝐴𝐵𝐷=𝑚∠𝐶𝐵𝐷,𝑚 ∠𝐴𝐷𝐵=𝑚∠𝐶𝐷𝐵.

Since the included side of these angles is shared between triangles △𝐷𝐵𝐶 and △𝐷𝐵𝐴, we know that 𝐵𝐷 is a common side and we can show that these triangles are congruent.

By the ASA criterion, we can conclude that △𝐷𝐵𝐶≅△𝐷𝐵𝐴. This means that their corresponding sides and angles must all be congruent. We can highlight the corresponding sides on the diagram.

We have 𝐶𝐵≅𝐴𝐵, so 𝐶𝐵=𝐴𝐵=20cm. Similarly, we have 𝐴𝐷≅𝐶𝐷, so 𝐴𝐷=𝐶𝐷=12cm.

Let’s finish by recapping some of the important points from this explainer.

Key Points

• We can use the congruency of triangles to prove geometric properties such as the property of the diagonals of a parallelogram bisecting each other.
• We can use the congruency of triangles to determine the lengths of missing sides and the measures of missing angles in some geometric constructions with triangles.